Average Number of Items on a Baby Registry

Metric in epidemiology

This article is almost the rate of spread of an epidemic. For the boilerplate number of offspring born to a female, run across Cyberspace reproduction rate.

"R number" redirects here. For other uses, see R-value.

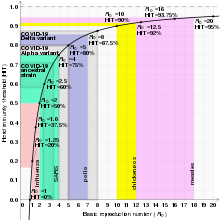
Graph of herd immunity threshold vs basic reproduction number with selected diseases

In epidemiology, the basic reproduction number, or basic reproductive number (sometimes called basic reproduction ratio or basic reproductive charge per unit), denoted ${\displaystyle R_{0}}$ (pronounced R nought or R zero),^[1] of an infection is the expected number of cases directly generated by ane case in a population where all individuals are susceptible to infection.^[2] The definition assumes that no other individuals are infected or immunized (naturally or through vaccination). Some definitions, such as that of the Australian Department of Health, add together the absence of "any deliberate intervention in disease transmission".^[iii] The basic reproduction number is not necessarily the same every bit the effective reproduction number ${\displaystyle R}$ (usually written ${\displaystyle R_{t}}$ [t for time], sometimes ${\displaystyle R_{due east}}$ ),^[4] which is the number of cases generated in the current land of a population, which does not have to be the uninfected land. ${\displaystyle R_{0}}$ is a dimensionless number (persons infected per person infecting) and not a time rate, which would have units of time⁻¹,^[five] or units of time like doubling time.^[6]

${\displaystyle R_{0}}$ is not a biological constant for a pathogen as it is also afflicted by other factors such equally environmental conditions and the behaviour of the infected population. ${\displaystyle R_{0}}$ values are usually estimated from mathematical models, and the estimated values are dependent on the model used and values of other parameters. Thus values given in the literature only make sense in the given context and information technology is recommended non to use obsolete values or compare values based on different models.^[seven] ${\displaystyle R_{0}}$ does not by itself requite an approximate of how fast an infection spreads in the population.

The most important uses of ${\displaystyle R_{0}}$ are determining if an emerging infectious illness can spread in a population and determining what proportion of the population should be immunized through vaccination to eradicate a disease. In commonly used infection models, when ${\displaystyle R_{0}>1}$ the infection will be able to offset spreading in a population, but non if ${\displaystyle R_{0}<1}$ . Generally, the larger the value of ${\displaystyle R_{0}}$ , the harder it is to control the epidemic. For uncomplicated models, the proportion of the population that needs to exist finer immunized (meaning not susceptible to infection) to prevent sustained spread of the infection has to exist larger than ${\displaystyle i-1/R_{0}}$ .^[viii] Conversely, the proportion of the population that remains susceptible to infection in the endemic equilibrium is ${\displaystyle 1/R_{0}}$ .

The basic reproduction number is affected by several factors, including the duration of infectivity of affected people, the infectiousness of the microorganism, and the number of susceptible people in the population that the infected people contact.

History [edit]

The roots of the basic reproduction concept can be traced through the work of Ronald Ross, Alfred Lotka and others,^[9] but its first mod application in epidemiology was by George Macdonald in 1952,^[x] who constructed population models of the spread of malaria. In his piece of work he called the quantity basic reproduction rate and denoted it past ${\displaystyle Z_{0}}$ . "Charge per unit" in this context ways per person, which makes ${\displaystyle Z_{0}}$ dimensionless as required. Because this tin can exist misleading to anyone who understands "rate" only in the sense per unit of time, "number" or "ratio" is at present preferred.^{[ citation needed ]}

Definitions in specific cases [edit]

Contact rate and infectious flow [edit]

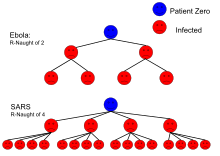
${\displaystyle R_{0}}$ is the average number of people infected from one other person. For example, Ebola has an ${\displaystyle R_{0}}$ of two, then on boilerplate, a person who has Ebola will pass it on to two other people.

Suppose that infectious individuals make an boilerplate of ${\displaystyle \beta }$ infection-producing contacts per unit time, with a mean infectious period of ${\displaystyle \tau }$ . Then the bones reproduction number is:

$${\displaystyle R_{0}=\beta \,\tau }$$

This unproblematic formula suggests unlike means of reducing ${\displaystyle R_{0}}$ and ultimately infection propagation. Information technology is possible to decrease the number of infection-producing contacts per unit fourth dimension ${\displaystyle \beta }$ by reducing the number of contacts per unit time (for example staying at dwelling house if the infection requires contact with others to propagate) or the proportion of contacts that produces infection (for example wearing some sort of protective equipment). Hence, it tin besides be written every bit^[eleven]

${\displaystyle R_{0}={\overline {c}}\,T\,\tau ,}$

where ${\displaystyle {\overline {c}}}$ is the rate of contact between susceptible and infected individuals and ${\displaystyle T}$ is the transmissibility, i.e, the probability of infection given a contact. It is also possible to decrease the infectious period ${\displaystyle \tau }$ by finding and and then isolating, treating or eliminating (equally is often the case with animals) infectious individuals as soon every bit possible.^{[ citation needed ]}

With varying latent periods [edit]

Latent period is the transition fourth dimension betwixt contagion event and illness manifestation. In cases of diseases with varying latent periods, the basic reproduction number can be calculated as the sum of the reproduction numbers for each transition time into the affliction. An case of this is tuberculosis (TB). Blower and coauthors calculated from a simple model of TB the following reproduction number:^[12]

$${\displaystyle R_{0}=R_{0}^{\text{FAST}}+R_{0}^{\text{Dull}}}$$

In their model, it is assumed that the infected individuals can develop active TB by either direct progression (the disease develops immediately after infection) considered in a higher place as FAST tuberculosis or endogenous reactivation (the disease develops years afterwards the infection) considered in a higher place every bit Tedious tuberculosis.^[13]

Heterogeneous populations [edit]

In populations that are not homogeneous, the definition of ${\displaystyle R_{0}}$ is more subtle. The definition must business relationship for the fact that a typical infected individual may not be an average individual. As an farthermost example, consider a population in which a small portion of the individuals mix fully with 1 some other while the remaining individuals are all isolated. A affliction may exist able to spread in the fully mixed portion even though a randomly selected individual would lead to fewer than one secondary case. This is because the typical infected individual is in the fully mixed portion and thus is able to successfully cause infections. In full general, if the individuals infected early in an epidemic are on boilerplate either more likely or less likely to transmit the infection than individuals infected late in the epidemic, then the ciphering of ${\displaystyle R_{0}}$ must business relationship for this difference. An advisable definition for ${\displaystyle R_{0}}$ in this case is "the expected number of secondary cases produced, in a completely susceptible population, produced past a typical infected individual".^[14]

The bones reproduction number can be computed every bit a ratio of known rates over time: if an infectious private contacts ${\displaystyle \beta }$ other people per unit time, if all of those people are assumed to contract the affliction, and if the disease has a hateful infectious period of ${\displaystyle {\dfrac {1}{\gamma }}}$ , and so the basic reproduction number is just ${\displaystyle R_{0}={\dfrac {\beta }{\gamma }}}$ . Some diseases have multiple possible latency periods, in which case the reproduction number for the disease overall is the sum of the reproduction number for each transition time into the affliction. For example, Blower et al.^[12] model 2 forms of tuberculosis infection: in the fast case, the symptoms show up immediately later exposure; in the slow case, the symptoms develop years after the initial exposure (endogenous reactivation). The overall reproduction number is the sum of the ii forms of contraction: ${\displaystyle R_{0}=R_{0}^{FAST}+R_{0}^{SLOW}}$ .

Estimation methods [edit]

The basic reproduction number can be estimated through examining detailed transmission chains or through genomic sequencing. However, it is most frequently calculated using epidemiological models.^[15] During an epidemic, typically the number of diagnosed infections ${\displaystyle N(t)}$ over time ${\displaystyle t}$ is known. In the early stages of an epidemic, growth is exponential, with a logarithmic growth charge per unit

$${\displaystyle K:={\frac {d\ln(Due north)}{dt}}.}$$

For exponential growth, ${\displaystyle N}$ tin be interpreted every bit the cumulative number of diagnoses (including individuals who accept recovered) or the present number of infection cases; the logarithmic growth charge per unit is the same for either definition. In order to estimate ${\displaystyle R_{0}}$ , assumptions are necessary about the fourth dimension filibuster betwixt infection and diagnosis and the time between infection and starting to be infectious.

In exponential growth, ${\displaystyle K}$ is related to the doubling time ${\displaystyle T_{d}}$ as

$${\displaystyle K={\frac {\ln(2)}{T_{d}}}.}$$

Uncomplicated model [edit]

If an private, after getting infected, infects exactly ${\displaystyle R_{0}}$ new individuals just afterwards exactly a fourth dimension ${\displaystyle \tau }$ (the series interval) has passed, and so the number of infectious individuals over time grows equally

$${\displaystyle n_{E}(t)=n_{Eastward}(0)\,R_{0}^{t/\tau }=n_{E}(0)\,east^{Kt}}$$

or

$${\displaystyle \ln(n_{Eastward}(t))=\ln(n_{E}(0))+\ln(R_{0})t/\tau .}$$

The underlying matching differential equation is

$${\displaystyle {\frac {dn_{Due east}(t)}{dt}}=n_{E}(t){\frac {\ln(R_{0})}{\tau }}.}$$

or

$${\displaystyle {\frac {d\ln(n_{East}(t))}{dt}}={\frac {\ln(R_{0})}{\tau }}.}$$

In this example, ${\displaystyle R_{0}=due east^{Yard\tau }}$ or ${\displaystyle K={\frac {\ln R_{0}}{\tau }}}$ .

For example, with ${\displaystyle \tau =5~\mathrm {d} }$ and ${\displaystyle K=0.183~\mathrm {d} ^{-ane}}$ , we would find ${\displaystyle R_{0}=2.five}$ .

If ${\displaystyle R_{0}}$ is fourth dimension dependent

$${\displaystyle \ln(n_{E}(t))=\ln(n_{Eastward}(0))+{\frac {1}{\tau }}\int \limits _{0}^{t}\ln(R_{0}(t))dt}$$

showing that it may be important to continue ${\displaystyle \ln(R_{0})}$ below 0, time-averaged, to avoid exponential growth.

Latent infectious period, isolation after diagnosis [edit]

In this model, an private infection has the following stages:

1. Exposed: an private is infected, but has no symptoms and does non all the same infect others. The average elapsing of the exposed land is ${\displaystyle \tau _{Eastward}}$ .
2. Latent infectious: an individual is infected, has no symptoms, but does infect others. The boilerplate elapsing of the latent infectious state is ${\displaystyle \tau _{I}}$ . The individual infects ${\displaystyle R_{0}}$ other individuals during this menstruum.
3. Isolation after diagnosis: measures are taken to foreclose further infections, for example by isolating the infected person.

This is a SEIR model and ${\displaystyle R_{0}}$ may exist written in the following course^[16]

$${\displaystyle R_{0}=1+Grand(\tau _{E}+\tau _{I})+Chiliad^{2}\tau _{E}\tau _{I}.}$$

This estimation method has been applied to COVID-nineteen and SARS. Information technology follows from the differential equation for the number of exposed individuals ${\displaystyle n_{East}}$ and the number of latent infectious individuals ${\displaystyle n_{I}}$ ,

$${\displaystyle {\frac {d}{dt}}{\begin{pmatrix}n_{East}\\n_{I}\terminate{pmatrix}}={\begin{pmatrix}-1/\tau _{E}&R_{0}/\tau _{I}\\1/\tau _{E}&-1/\tau _{I}\end{pmatrix}}{\begin{pmatrix}n_{Due east}\\n_{I}\end{pmatrix}}.}$$

The largest eigenvalue of the matrix is the logarithmic growth rate ${\displaystyle K}$ , which can be solved for ${\displaystyle R_{0}}$ .

In the special case ${\displaystyle \tau _{I}=0}$ , this model results in ${\displaystyle R_{0}=i+K\tau _{E}}$ , which is different from the elementary model above ( ${\displaystyle R_{0}=\exp(K\tau _{E})}$ ). For case, with the same values ${\displaystyle \tau =5~\mathrm {d} }$ and ${\displaystyle K=0.183~\mathrm {d} ^{-1}}$ , we would find ${\displaystyle R_{0}=ane.9}$ , rather than the truthful value of ${\displaystyle two.5}$ . The divergence is due to a subtle difference in the underlying growth model; the matrix equation to a higher place assumes that newly infected patients are currently already contributing to infections, while in fact infections only occur due to the number infected at ${\displaystyle \tau _{E}}$ agone. A more than correct treatment would require the use of delay differential equations.^[17]

Effective reproduction number [edit]

An caption of the ${\displaystyle R}$ number in simple terms from the Welsh Government.

In reality, varying proportions of the population are immune to whatever given disease at any given fourth dimension. To account for this, the effective reproduction number ${\displaystyle R_{eastward}}$ or ${\displaystyle R}$ is used. ${\displaystyle R_{t}}$ is the average number of new infections caused by a single infected individual at time t in the partially susceptible population. Information technology tin exist found by multiplying ${\displaystyle R_{0}}$ by the fraction S of the population that is susceptible. When the fraction of the population that is allowed increases (i. east. the susceptible population S decreases) and so much that ${\displaystyle R_{e}}$ drops beneath i in a bones SIR simulation, "herd amnesty" has been accomplished and the number of cases occurring in the population will gradually subtract to zero.^{[xviii] [19] [20]}

Limitations of R ₀ [edit]

Utilise of ${\displaystyle R_{0}}$ in the popular press has led to misunderstandings and distortions of its significant. ${\displaystyle R_{0}}$ can be calculated from many unlike mathematical models. Each of these can requite a dissimilar estimate of ${\displaystyle R_{0}}$ , which needs to be interpreted in the context of that model. Therefore, the contagiousness of different infectious agents cannot exist compared without recalculating ${\displaystyle R_{0}}$ with invariant assumptions. ${\displaystyle R_{0}}$ values for past outbreaks might non be valid for current outbreaks of the same disease. Generally speaking, ${\displaystyle R_{0}}$ tin be used as a threshold, fifty-fifty if calculated with different methods: if ${\displaystyle R_{0}<1}$ , the outbreak will die out, and if ${\displaystyle R_{0}>ane}$ , the outbreak will expand. In some cases, for some models, values of ${\displaystyle R_{0}<1}$ can still lead to self-perpetuating outbreaks. This is especially problematic if in that location are intermediate vectors between hosts, such as malaria.^[21] Therefore, comparisons between values from the "Values of ${\displaystyle R_{0}}$ of well-known infectious diseases" table should exist conducted with caution.

Although ${\displaystyle R_{0}}$ cannot be modified through vaccination or other changes in population susceptibility, it can vary based on a number of biological, sociobehavioral, and environmental factors.^[7] Information technology can also be modified by physical distancing and other public policy or social interventions,^{[22] [seven]} although some historical definitions exclude any deliberate intervention in reducing disease transmission, including nonpharmacological interventions.^[three] And indeed, whether nonpharmacological interventions are included in ${\displaystyle R_{0}}$ often depends on the paper, disease, and what if whatever intervention is being studied.^[7] This creates some confusion, because ${\displaystyle R_{0}}$ is not a constant; whereas virtually mathematical parameters with "nought" subscripts are constants.

${\displaystyle R}$ depends on many factors, many of which need to be estimated. Each of these factors adds to uncertainty in estimates of ${\displaystyle R}$ . Many of these factors are not important for informing public policy. Therefore, public policy may be better served by metrics similar to ${\displaystyle R}$ , merely which are more straightforward to estimate, such as doubling fourth dimension or half-life ( ${\displaystyle t_{1/2}}$ ).^{[23] [24]}

Methods used to calculate ${\displaystyle R_{0}}$ include the survival function, rearranging the largest eigenvalue of the Jacobian matrix, the next-generation method,^[25] calculations from the intrinsic growth rate,^[26] being of the owned equilibrium, the number of susceptibles at the endemic equilibrium, the boilerplate age of infection^[27] and the last size equation. Few of these methods concur with one another, fifty-fifty when starting with the same arrangement of differential equations.^[21] Fifty-fifty fewer actually summate the average number of secondary infections. Since ${\displaystyle R_{0}}$ is rarely observed in the field and is usually calculated via a mathematical model, this severely limits its usefulness.^[28]

Sample values for various infectious diseases [edit]

Values of R ₀ and herd immunity thresholds (HITs) of well-known infectious diseases prior to intervention

Affliction	Transmission	R 0	HIT[a]
Measles	Droplets	12–18[29] [7]	92–94%
Chickenpox (varicella)	Aerosol	10–12[30]	ninety–92%
Mumps	Respiratory droplets	10–12[31]	ninety–92%
Rubella	Respiratory aerosol	half dozen–7[b]	83–86%
Polio	Fecal–oral road	v–7[b]	fourscore–86%
Pertussis	Respiratory droplets	5.5[36]	82%
COVID-19 (Delta variant)	Respiratory droplets and aerosol	five.1[37]	fourscore%
Smallpox	Respiratory droplets	3.5–half-dozen.0[38]	71–83%
COVID-nineteen (Blastoff variant)	Respiratory droplets and aerosol	4–v[39] [ medical citation needed ]	75–fourscore%
HIV/AIDS	Body fluids	2–5[xl]	l–lxxx%
COVID-19 (ancestral strain)	Respiratory droplets and aerosol[41]	2.9 ( 2.4– 3.4 )[42]	65% ( 58– 71% )
SARS	Respiratory droplets	two–iv[43]	fifty–75%
Diphtheria	Saliva	two.six ( 1.7– four.three )[44]	62% ( 41– 77% )
Mutual cold	Respiratory droplets	2–3[45] [ medical citation needed ]	50–67%
Influenza (1918 pandemic strain)	Respiratory droplets	2[46]	50%
Ebola (2014 outbreak)	Trunk fluids	1.eight ( 1.4– 1.8 )[47]	44% ( 31– 44% )
Influenza (2009 pandemic strain)	Respiratory droplets	1.half-dozen ( i.three– 2.0 )[2]	37% ( 25– 51% )
Flu (seasonal strains)	Respiratory droplets	1.three ( 1.2– 1.4 )[48]	23% ( 17– 29% )
Andes hantavirus	Respiratory droplets and body fluids	1.ii ( 0.eight– i.6 )[49]	16% ( 0– 36% )[c]
Nipah virus	Torso fluids	0.5[50]	0%[c]
MERS	Respiratory droplets	0.5 ( 0.iii– 0.eight )[51]	0%[c]

In popular civilization [edit]

In the 2011 film Contamination, a fictional medical disaster thriller, a blogger'south calculations for ${\displaystyle R_{0}}$ are presented to reflect the progression of a fatal viral infection from example studies to a pandemic. The methods depicted were faulty.^[22]

See also [edit]

• Compartmental models in epidemiology
• East-epidemiology
• Epi Info software program
• Epidemiological method
• Epidemiological transition

Notes [edit]

1. ^ Calculated using p = one − 1 / R ₀ .
2. ^ ^{a b} From a module of a training class^[32] with information modified from other sources.^{[33] [34] [35]}
3. ^ ^{a b c} When R₀ < 1.0, the disease naturally disappears.

• Compartmental models in epidemiology describe disease dynamics over time in a population of susceptible (S), infectious (I), and recovered (R) people using the SIR model. Note that in the SIR model, ${\displaystyle R(0)}$ and ${\displaystyle R_{0}}$ are different quantities – the former describes the number of recovered at t = 0 whereas the latter describes the ratio between the frequency of contacts to the frequency of recovery.
• Held 50, Hens Due north, O'Neill PD, Wallinga J (November 7, 2019). Handbook of Infectious Disease Data Assay. CRC Press. p. 347. ISBN978-one-351-83932-7. According to Guangdong Provincial Center for Disease Control and Prevention, "The effective reproductive number (R or R_{due east} is more commonly used to describe transmissibility, which is defined as the boilerplate number of secondary cases generated by per [sic] infectious case." For example, by one preliminary gauge during the ongoing pandemic, the effective reproductive number for SARS-CoV-2 was found to exist 2.9,^{[ citation needed ]} whereas for SARS it was 1.77.

References [edit]

1. ^ Milligan GN, Barrett AD (2015). Vaccinology : an essential guide. Chichester, West Sussex: Wiley Blackwell. p. 310. ISBN978-i-118-63652-seven. OCLC 881386962.
2. ^ ^{a b} Fraser C, Donnelly CA, Cauchemez S, Hanage WP, Van Kerkhove MD, Hollingsworth TD, et al. (June 2009). "Pandemic potential of a strain of influenza A (H1N1): early findings". Science. 324 (5934): 1557–61. Bibcode:2009Sci...324.1557F. doi:x.1126/science.1176062. PMC3735127. PMID 19433588.
3. ^ ^{a b} Becker NG, Glass Yard, Barnes B, Caley P, Philp D, McCaw JM, et al. (April 2006). "The reproduction number". Using Mathematical Models to Assess Responses to an Outbreak of an Emerged Viral Respiratory Disease. National Centre for Epidemiology and Population Wellness. ISBN1-74186-357-0 . Retrieved February 1, 2020.
4. ^ Adam D (July 2020). "A guide to R - the pandemic's misunderstood metric". Nature. 583 (7816): 346–348. Bibcode:2020Natur.583..346A. doi:x.1038/d41586-020-02009-west. PMID 32620883.
5. ^ Jones J. "Notes On R0" (PDF). Stanford University.
6. ^ Siegel E. "Why 'Exponential Growth' Is So Scary For The COVID-19 Coronavirus". Forbes . Retrieved March 19, 2020.
7. ^ ^{a b c d e} Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH (Jan 2019). "Complication of the Basic Reproduction Number (R₀)". Emerging Infectious Diseases. 25 (1): 1–4. doi:10.3201/eid2501.171901. PMC6302597. PMID 30560777.
8. ^ Fine, P.; Eames, K.; Heymann, D. 50. (April 1, 2011). "'Herd Immunity': A Rough Guide". Clinical Infectious Diseases. 52 (7): 911–916. doi:10.1093/cid/cir007. PMID 21427399.
9. ^ Smith DL, Battle KE, Hay SI, Barker CM, Scott TW, McKenzie FE (April five, 2012). "Ross, macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens". PLOS Pathogens. 8 (iv): e1002588. doi:10.1371/journal.ppat.1002588. PMC3320609. PMID 22496640.
10. ^ Macdonald K (September 1952). "The assay of equilibrium in malaria". Tropical Diseases Message. 49 (9): 813–29. PMID 12995455.
11. ^ J.H. Jones, Notes on R₀. Stanford University (2007).
12. ^ ^{a b} Blower SM, McLean AR, Porco TC, Small PM, Hopewell PC, Sanchez MA, Moss AR (August 1995). "The intrinsic manual dynamics of tuberculosis epidemics". Nature Medicine. i (8): 815–21. doi:x.1038/nm0895-815. PMID 7585186. S2CID 19795498.
13. ^ Ma Y, Horsburgh CR, White LF, Jenkins HE (September 2018). "Quantifying TB transmission: a systematic review of reproduction number and serial interval estimates for tuberculosis". Epidemiology and Infection. 146 (12): 1478–1494. doi:x.1017/S0950268818001760. PMC6092233. PMID 29970199.
14. ^ Diekmann O, Heesterbeek JA, Metz JA (1990). "On the definition and the ciphering of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations". Journal of Mathematical Biology. 28 (4): 365–82. doi:ten.1007/BF00178324. hdl:1874/8051. PMID 2117040. S2CID 22275430.
15. ^ Wohl South, Schaffner SF, Sabeti PC (September 2016). "Genomic Analysis of Viral Outbreaks". Annual Review of Virology. 3 (i): 173–195. doi:ten.1146/annurev-virology-110615-035747. PMC5210220. PMID 27501264.
16. ^ Lipsitch Grand, Cohen T, Cooper B, Robins JM, Ma Southward, James L, et al. (June 2003). "Transmission dynamics and control of severe acute respiratory syndrome". Science. 300 (5627): 1966–lxx. Bibcode:2003Sci...300.1966L. doi:10.1126/science.1086616. PMC2760158. PMID 12766207.
17. ^ Rihan, Fathalla A.; Anwar, Chiliad. Naim (2012). "Qualitative Analysis of Delayed SIR Epidemic Model with a Saturated Incidence Rate". International Journal of Differential Equations. 2012: 1–13. doi:10.1155/2012/408637.
18. ^ Garnett GP (February 2005). "Role of herd immunity in determining the effect of vaccines against sexually transmitted illness". The Periodical of Infectious Diseases. 191 (Suppl 1): S97-106. doi:10.1086/425271. PMID 15627236.
19. ^ Rodpothong P, Auewarakul P (October 2012). "Viral development and manual effectiveness". World Periodical of Virology. 1 (v): 131–four. doi:10.5501/wjv.v1.i5.131. PMC3782273. PMID 24175217.
20. ^ Dabbaghian 5, Mago VK (2013). Theories and Simulations of Circuitous Social Systems. Springer. pp. 134–35. ISBN978-3642391491 . Retrieved March 29, 2015.
21. ^ ^{a b} Li J, Blakeley D, Smith RJ (2011). "The failure of R0". Computational and Mathematical Methods in Medicine. 2011 (527610): 527610. doi:10.1155/2011/527610. PMC3157160. PMID 21860658.
22. ^ ^{a b} Byrne M (October vi, 2014), "The Misunderstood Number That Predicts Epidemics", vice.com , retrieved March 23, 2020
23. ^ Balkew TM (December 2010). The SIR Model When S(t) is a Multi-Exponential Function (Thesis). East Tennessee State University.
24. ^ Ireland MW, ed. (1928). The Medical Section of the United states of america Army in the Globe War, vol. IX: Communicable and Other Diseases. Washington: U.Due south.: U.S. Government Printing Office. pp. 116–7.
25. ^ Diekmann O, Heesterbeek JA (2000). "The Basic Reproduction Ratio". Mathematical Epidemiology of Infectious Diseases : Model Edifice, Analysis and Interpretation. New York: Wiley. pp. 73–98. ISBN0-471-49241-8.
26. ^ Chowell 1000, Hengartner NW, Castillo-Chavez C, Fenimore Pow, Hyman JM (July 2004). "The basic reproductive number of Ebola and the furnishings of public wellness measures: the cases of Congo and Uganda". Journal of Theoretical Biological science. 229 (i): 119–26. arXiv:q-bio/0503006. Bibcode:2004JThBi.229..119C. doi:10.1016/j.jtbi.2004.03.006. PMID 15178190. S2CID 7298792.
27. ^ Ajelli One thousand, Iannelli M, Manfredi P, Ciofi degli Atti ML (March 2008). "Basic mathematical models for the temporal dynamics of HAV in medium-endemicity Italian areas". Vaccine. 26 (xiii): 1697–707. doi:10.1016/j.vaccine.2007.12.058. PMID 18314231.
28. ^ Heffernan JM, Smith RJ, Wahl LM (September 2005). "Perspectives on the bones reproductive ratio". Journal of the Imperial Society, Interface. 2 (4): 281–93. doi:10.1098/rsif.2005.0042. PMC1578275. PMID 16849186.
29. ^ Guerra FM, Bolotin S, Lim Thou, Heffernan J, Deeks SL, Li Y, Crowcroft NS (December 2017). "The bones reproduction number (R₀) of measles: a systematic review". The Lancet. Infectious Diseases. 17 (12): e420–e428. doi:10.1016/S1473-3099(17)30307-9. PMID 28757186.
30. ^ Ireland's Health Services. Wellness Care Worker Information (PDF) . Retrieved March 27, 2020.
31. ^ Australian government Section of Health Mumps Laboratory Example Definition (LCD)
32. ^ Centers for Disease Control and Prevention; Earth Wellness Organization (2001). "History and epidemiology of global smallpox eradication". Smallpox: disease, prevention, and intervention (training course) (Presentation). Atlanta: Centers for Disease Control and Prevention (published August 25, 2014). cdc:27929. Archived (PDF) from the original on March 17, 2017. Retrieved June 17, 2021.
33. ^ Fine, Paul E. G. (1993). "Herd Immunity: History, Theory, Practice". Epidemiologic Reviews. xv (2): 265–302. doi:10.1093/oxfordjournals.epirev.a036121. PMID 8174658.
34. ^ Luman, ET; Barker, LE; Simpson, DM; Rodewald, LE; Szilagyi, PG; Zhao, Z (May 2001). "National, state, and urban-area vaccination-coverage levels among children aged 19–35 months, United States, 1999". American Periodical of Preventive Medicine. 20 (4): 88–153. doi:10.1016/s0749-3797(01)00274-4. PMID 12174806.
35. ^ Jiles, RB; Fuchs, C; Klevens, RM (September 22, 2000). "Vaccination coverage amid children enrolled in Caput Beginning programs or twenty-four hour period care facilities or inbound schoolhouse". Morbidity and Mortality Weekly Report. 49 (9): 27–38. PMID 11016876.
36. ^ Kretzschmar One thousand, Teunis PF, Pebody RG (June 2010). "Incidence and reproduction numbers of pertussis: estimates from serological and social contact data in v European countries". PLOS Medicine. seven (6): e1000291. doi:10.1371/journal.pmed.1000291. PMC2889930. PMID 20585374.
37. ^ Liu, Ying; Rocklöv, Joacim (October 1, 2021). "The reproductive number of the Delta variant of SARS-CoV-ii is far higher compared to the ancestral SARS-CoV-2 virus". Journal of Travel Medicine. 28 (7). doi:10.1093/jtm/taab124. ISSN 1708-8305. PMC8436367. PMID 34369565.
38. ^ Gani R, Leach S (Dec 2001). "Transmission potential of smallpox in contemporary populations". Nature. 414 (6865): 748–51. Bibcode:2001Natur.414..748G. doi:x.1038/414748a. PMID 11742399. S2CID 52799168. Retrieved March 18, 2020.
39. ^ Gallagher, James (June 12, 2021). "Covid: Is there a limit to how much worse variants can get?". BBC News . Retrieved July 21, 2021.
40. ^ "Playing the Numbers Game: R0". National Emerging Special Pathogen Grooming and Education Centre. Archived from the original on May 12, 202. Retrieved Dec 27, 2020. [...] while infections that require sexual contact like HIV have a lower R₀ (two-5).
41. ^ Prather, Kimberly A.; Marr, Linsey C.; Schooley, Robert T.; McDiarmid, Melissa A.; Wilson, Mary E.; Milton, Donald K. (October sixteen, 2020). "Airborne manual of SARS-CoV-2". Science. 370 (6514): 303.2–304. Bibcode:2020Sci...370..303P. doi:10.1126/science.abf0521. PMID 33020250. S2CID 222145689.
42. ^ Billah, Arif; Miah, Mamun; Khan, Nuruzzaman (November 11, 2020). "Reproductive number of coronavirus: A systematic review and meta-analysis based on global level evidence". PLOS ONE. 15 (11): e0242128. Bibcode:2020PLoSO..1542128B. doi:10.1371/journal.pone.0242128. PMC7657547. PMID 33175914.
43. ^ Consensus certificate on the epidemiology of severe acute respiratory syndrome (SARS). Section of Communicable Disease Surveillance and Response (Technical report). World Health Organization. p. 26. hdl:10665/70863. WHO/CDS/CSR/GAR/2003.11. A number of researchers have estimated the basic reproduction number by fitting models to the initial growth of epidemics in a number of countries. Their observations indicate that the SARS-CoV is less transmissible than initially thought with estimates of Ro in the range of 2-4.
44. ^ Truelove SA, Keegan LT, Moss WJ, Chaisson LH, Macher E, Azman As, Lessler J (June 2020). "Clinical and Epidemiological Aspects of Diphtheria: A Systematic Review and Pooled Analysis". Clinical Infectious Diseases. 71 (1): 89–97. doi:x.1093/cid/ciz808. PMC7312233. PMID 31425581.
45. ^ Freeman C. "Magic formula that volition determine whether Ebola is beaten". The Telegraph. Telegraph.Co.Uk. Archived from the original on January 12, 2022. Retrieved March xxx, 2020.
46. ^ "Omicron transmission: how contagious diseases spread". Nebraska Medicine. December 21, 2021. Retrieved January 25, 2022.
47. ^ Wong ZS, Bui CM, Chughtai AA, Macintyre CR (April 2017). "A systematic review of early modelling studies of Ebola virus disease in Due west Africa". Epidemiology and Infection. 145 (6): 1069–1094. doi:ten.1017/S0950268817000164. PMID 28166851. The median of the R₀ mean estimate for the ongoing epidemic (overall) is one.78 (interquartile range: 1.44, ane.80)
48. ^ Chowell G, Miller MA, Viboud C (June 2008). "Seasonal influenza in the United States, French republic, and Australia: transmission and prospects for control". Epidemiology and Infection. Cambridge University Press. 136 (6): 852–64. doi:10.1017/S0950268807009144. PMC2680121. PMID 17634159. The reproduction number across influenza seasons and countries lied in the range 0.ix–ii.0 with an overall mean of one.3, and 95% confidence interval (CI) ane.2–1.4.
49. ^ Martínez, Valeria P.; Di Paola, Nicholas; Alonso, Daniel O.; Pérez-Sautu, Unai; Bellomo, Carla 1000.; Iglesias, Ayelén A.; et al. (December three, 2020). "'Super-Spreaders' and Person-to-Person Transmission of Andes Virus in Argentina". New England Periodical of Medicine. 383 (23): 2230–2241. doi:10.1056/NEJMoa2009040. PMID 33264545. S2CID 227259435.
50. ^ Luby SP (October 2013). "The pandemic potential of Nipah virus". Antiviral Enquiry. 100 (ane): 38–43. doi:10.1016/j.antiviral.2013.07.011. PMID 23911335.
51. ^ Kucharski AJ, Althaus CL (June 2015). "The role of superspreading in Centre East respiratory syndrome coronavirus (MERS-CoV) transmission". Euro Surveillance. 20 (25): 14–8. doi:ten.2807/1560-7917.ES2015.twenty.25.21167. PMID 26132768.

Further reading [edit]

• Heesterbeek, J.A.P. (2002). "A cursory history of R0 and a recipe for its calculation". Acta Biotheoretica. 50 (3): 189–204. doi:ten.1023/a:1016599411804. hdl:1874/383700. PMID 12211331. S2CID 10178944.
• Heffernan, J.M; Smith, R.J; Wahl, Fifty.Chiliad (September 22, 2005). "Perspectives on the basic reproductive ratio". Journal of the Royal Order Interface. two (4): 281–293. doi:10.1098/rsif.2005.0042. PMC1578275. PMID 16849186.
• Jones JH (May 1, 2007). "Notes on ${\displaystyle R_{0}}$ " (PDF) . Retrieved November 6, 2018.
• Van Den Driessche, P.; Watmough, James (2008). "Farther Notes on the Basic Reproduction Number". Mathematical Epidemiology. Lecture Notes in Mathematics. Vol. 1945. pp. 159–178. doi:10.1007/978-3-540-78911-6_6. ISBN978-iii-540-78910-9.

Average Number of Items on a Baby Registry

Source: https://en.wikipedia.org/wiki/Basic_reproduction_number

Share this post